Zusammenfassender Überblick über Skalarprodukt, Kreuzprodukt und Spatprodukt;
die Hessesche Normal(en)form der Ebenengleichung
Definition: Skalarprodukt
("inneres Produkt")
Für zwei Vektoren a,b des Raumes R3 mit a = ( a1| a2 | a3 )T und b = ( b1| b2 | b3 )T definiert man:
a * b := a1b1+a2b2+a3b3.
Der erhaltene Wert wird als Skalarprodukt von a und b bezeichnet
(das Ergebnis ist kein Vektor, sondern eine reelle Zahl).
Die geometrische Bedeutung:
Schließen die Vektoren a und b ( nicht der Nullvektor)
den Winkel alpha ein, so gilt:
a * b = || a || . || b || . cos ( alpha ).
Definition: Kreuzprodukt ("äußeres
Produkt")
Für zwei Vektoren a,b des Raumes R3 mit a = ( a1 | a2
| a3 )T und b = ( b1 | b2|
b3 )T definiert man:
a x b =: ( a2b3 - a3b2 | a3b1 - a1b3 | a1b2 - a2b1)T
Der erhaltene Vektor wird als Kreuzprodukt der Vektoren a und
b bezeichnet.
Die geometrische Bedeutung:
Schließen die Vektoren a, b ( nicht der Nullvektor) den
Winkel beta ein, so gilt:
|| a x b || = || a || || b || |sin (beta)|.
Der Vektor a x b ist zu a und b orthogonal.
a , b, a x b bilden in der angegebenen Reihenfolge
ein Rechtssystem.
|| a x b || ist der Flächeninhalt des von a und b aufgespannten
Parallelogramms.

Definition: Spatprodukt
Für drei Vektoren a, b, c des Raumes R3 mit a = ( a1
| a2 | a3 )T, b = ( b1
| b2 | b3 )T und c = ( c1
| c2 | c 3 )T definiert man:
[ a b
c ] := a * ( b x c )
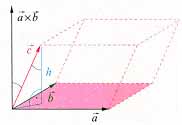
Die geometrische Bedeutung:
Der Ausdruck a * ( b x c ) beschreibt das Volumen (
oder die Gegenzahl des Volumens) vom
durch a, b, c aufgespannten Spats.
Definition: Normieren eines Vektors
Für a aus R3 ( nicht der Nullvektor) definiert man a0 := (1 / || a || ) a
Der Vektor a0 hat die Norm 1. Den Übergang von a zu a0 bezeichnet man als Normieren von a.
Definition: Hessesche Normalenform
Voraussetzung:
E Ebene durch A, B, C
(gegeben durch die Vektoren a, b, c; a, b,
c nicht kollinear),
P Punkt, gegeben durch seinen Ortsvektor p
n sei ein Normalenvektorvon E, also ein von o verschiedener Vektor, der orthogonal zu b-a und c-a ist.
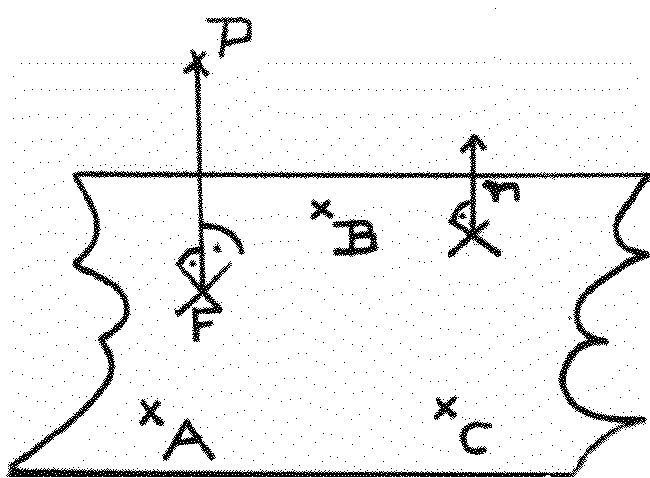
n = ( b - a ) x ( c - a ); F sei der Fußpunkt des von P auf E gefällten Lotes:
Falls || n || = 1 ist und die d die Länge Strecke PF ist, ergibt sich:
p - f = d n;
daraus folgt: f = p - d n
( p - f ) * ( a - f ) = 0
d n * ( a - p + d n) = 0
n * ( a - p ) + d n * n = 0
wegen || n || = 1 gilt:
n * ( p - a ) = d
Ergebnis:
Wenn A ein Punkt der Ebene E und n der normierte Normalenvektor von E ist, dann ergibt n * ( y - a ) den
Abstand, den der Punkt x von E hat, oder seine Gegenzahl.
Die Gleichung n * ( x - a ) = 0 heißt
dann Hessesche Normalenform der Ebenengleichung von E.


